利用离散时间系统实现连续时间系统

Posted 28/03/2024

By Jo Cruise 4 min read

问题描述

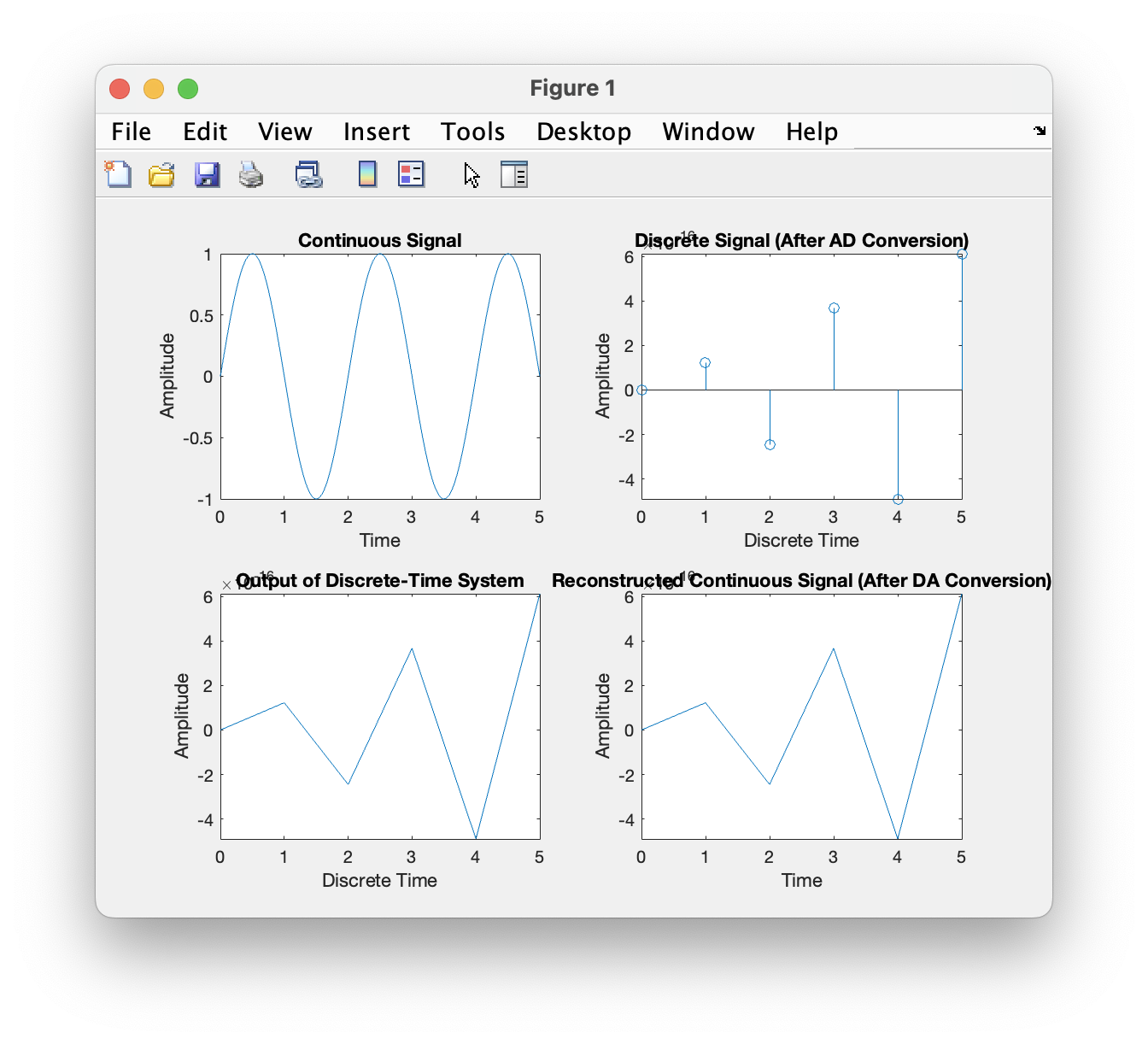
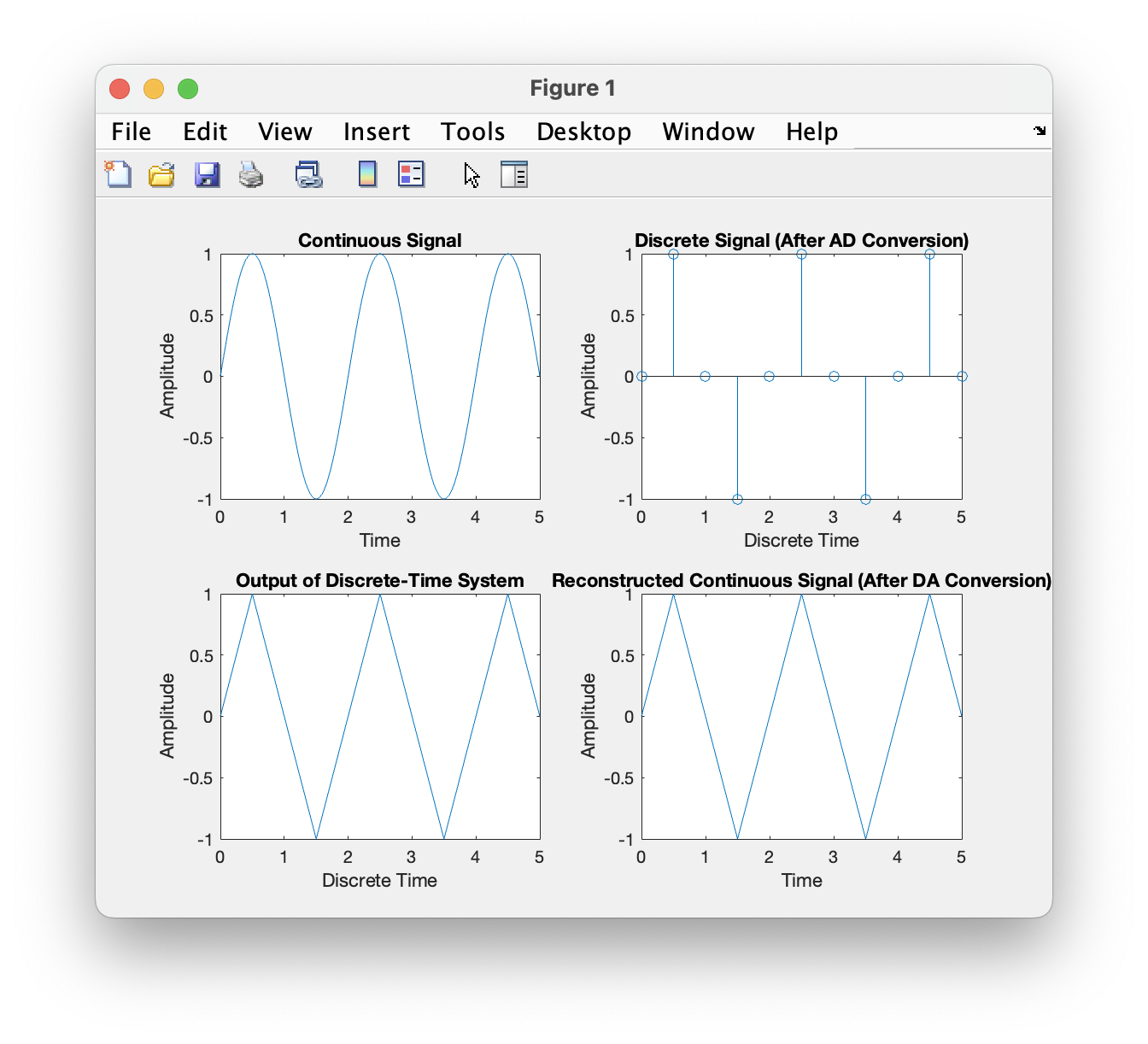
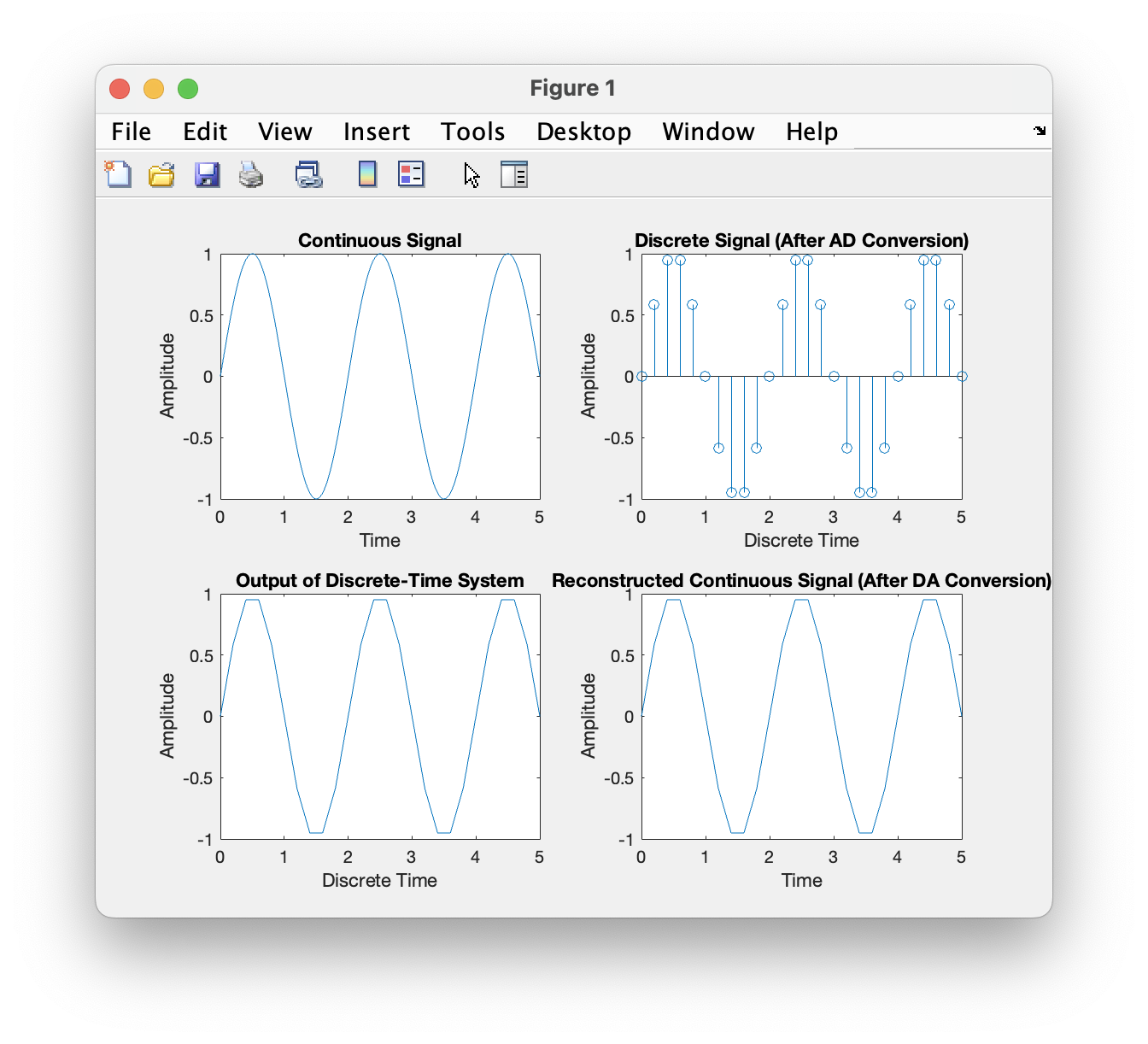
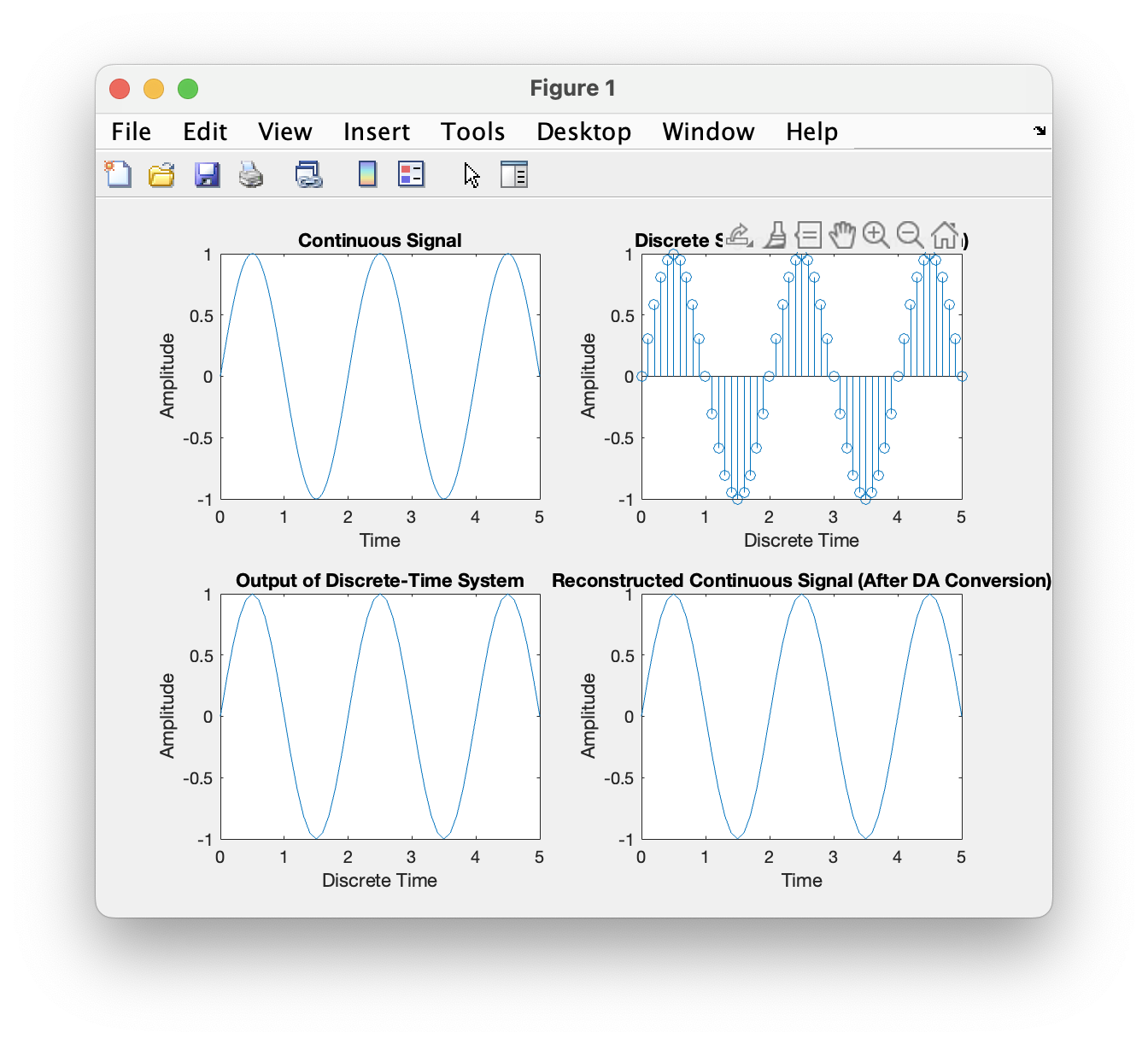
利用离散时间系统实现连续时间系统。 1) 如图 (a)所示为一个连续时间系统。 2) 图 (b)为连续信号经过 AD 变换变为离散信号，通过离散时间系统，然后经过 DA 变换变为连续信号。 3) 对上述 2 种方法进行仿真比较。并探究什么时候 2 种方法的输出结果是一致的。

提示:Matlab 编程实现中都是针对的离散信号，可以用较短的时间间隔来表示连续信号，用较长的时间间隔来表示离散信号。

理论引入

在学《数字电子技术基础》的时候我们知道Nyquist-Shannon sampling theorem，当采样率至少是信号带宽的两倍，输出信号可避免重叠。那么最佳采样值可参考其进行选取。

解决方法

讨论一

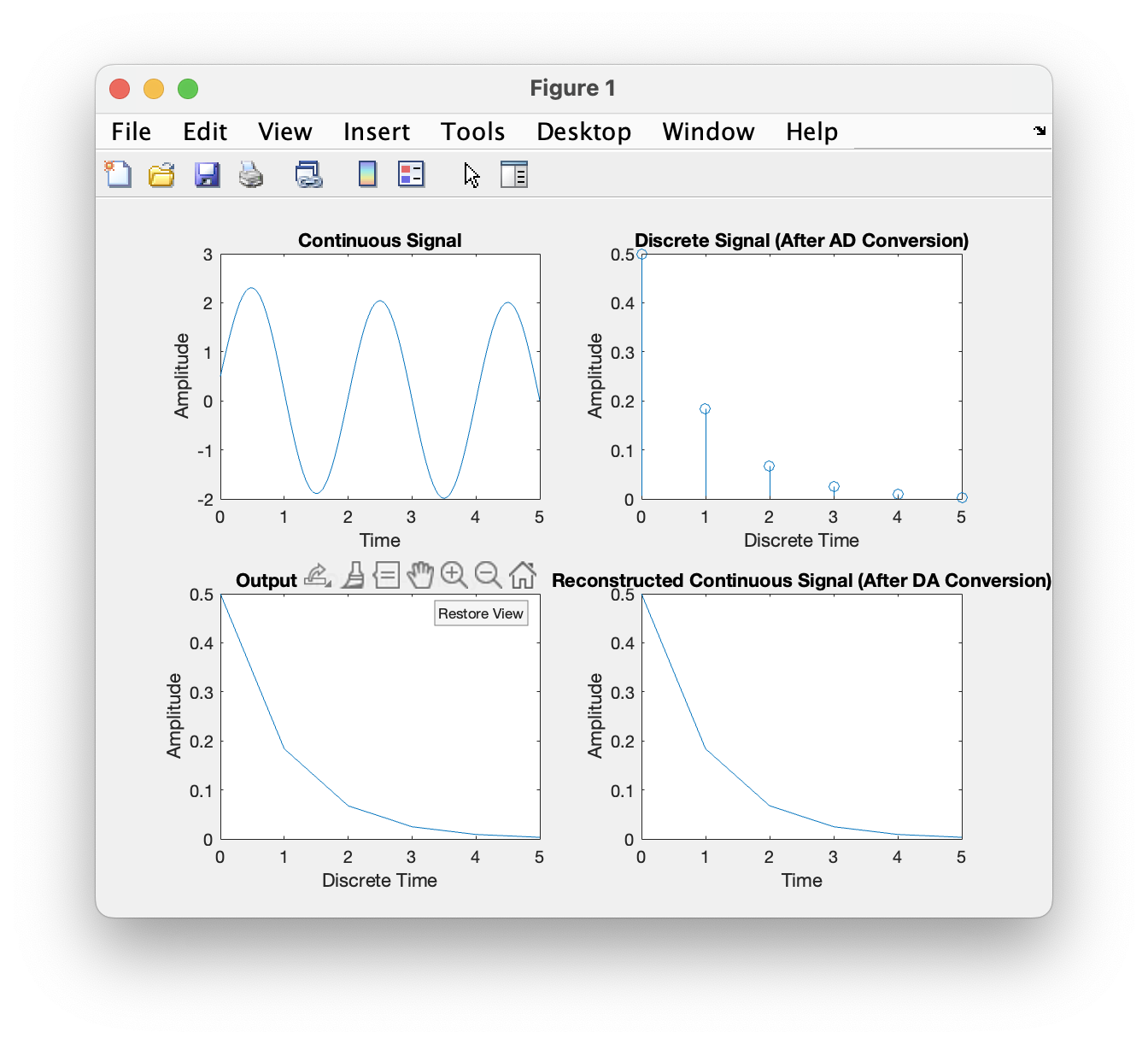
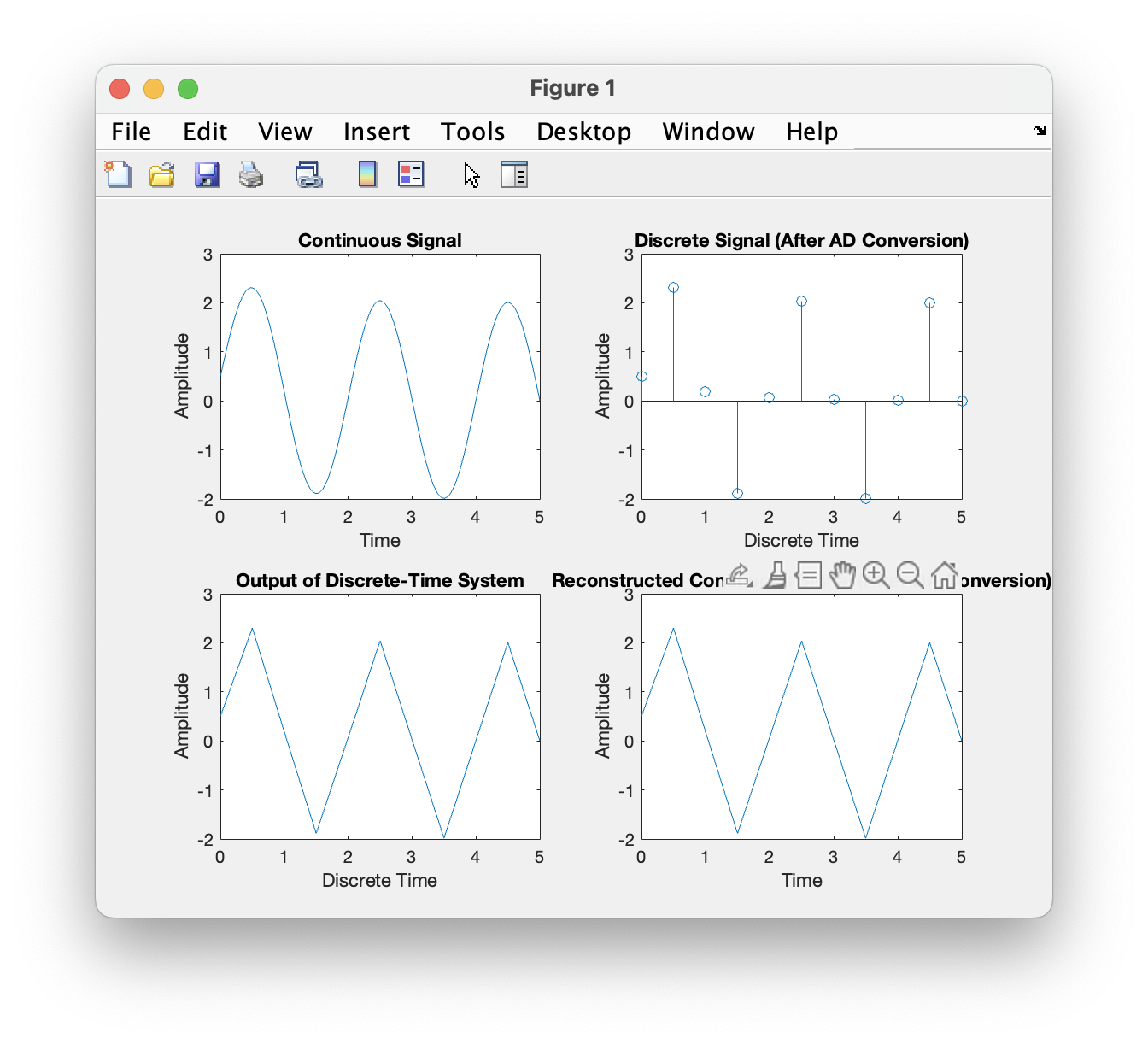
先讨论简单情况，当$x(t) = \sin t$，$h(t) = \delta(t)$时，$y(t) = \sin t$

  
t = 0:0.001:5; % 时间范围
f = 1/2; % 信号频率
x = sin(2*pi*f*t); % 连续信号

fs = 2; % 采样率
Ts = 1/fs; % 采样周期
n = 0:Ts:5; % 离散时间范围
xd = sin(2*pi*f*n); % 离散信号

t_interp = 0:0.01:5; % 插值时间范围
y = interp1(n, xd, t_interp, 'linear'); % 线性插值

% 绘制连续信号
figure;
subplot(2,2,1);
plot(t, x);
title('Continuous Signal');
xlabel('Time');
ylabel('Amplitude');

% 进行AD转换（模拟到数字）
subplot(2,2,2);
stem(n, xd);
title('Discrete Signal (After AD Conversion)');
xlabel('Discrete Time');
ylabel('Amplitude');

% 设计离散时间系统
subplot(2,2,3);
plot(n, xd);
title('Output of Discrete-Time System');
xlabel('Discrete Time');
ylabel('Amplitude');

% 进行DA转换（数字到模拟）
subplot(2,2,4);
plot(t_interp, y);
title('Reconstructed Continuous Signal (After DA Conversion)');
xlabel('Time');
ylabel('Amplitude');

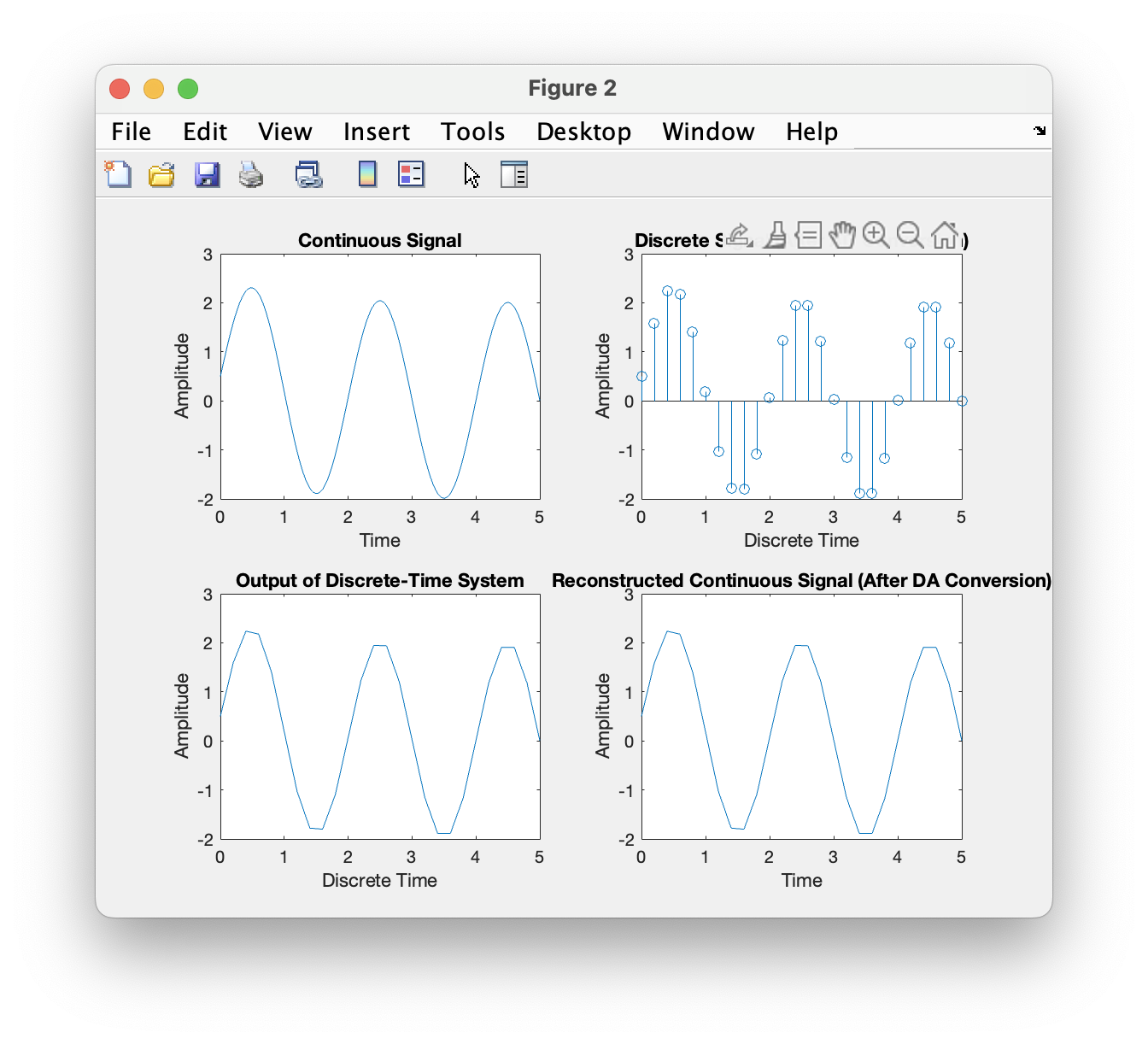
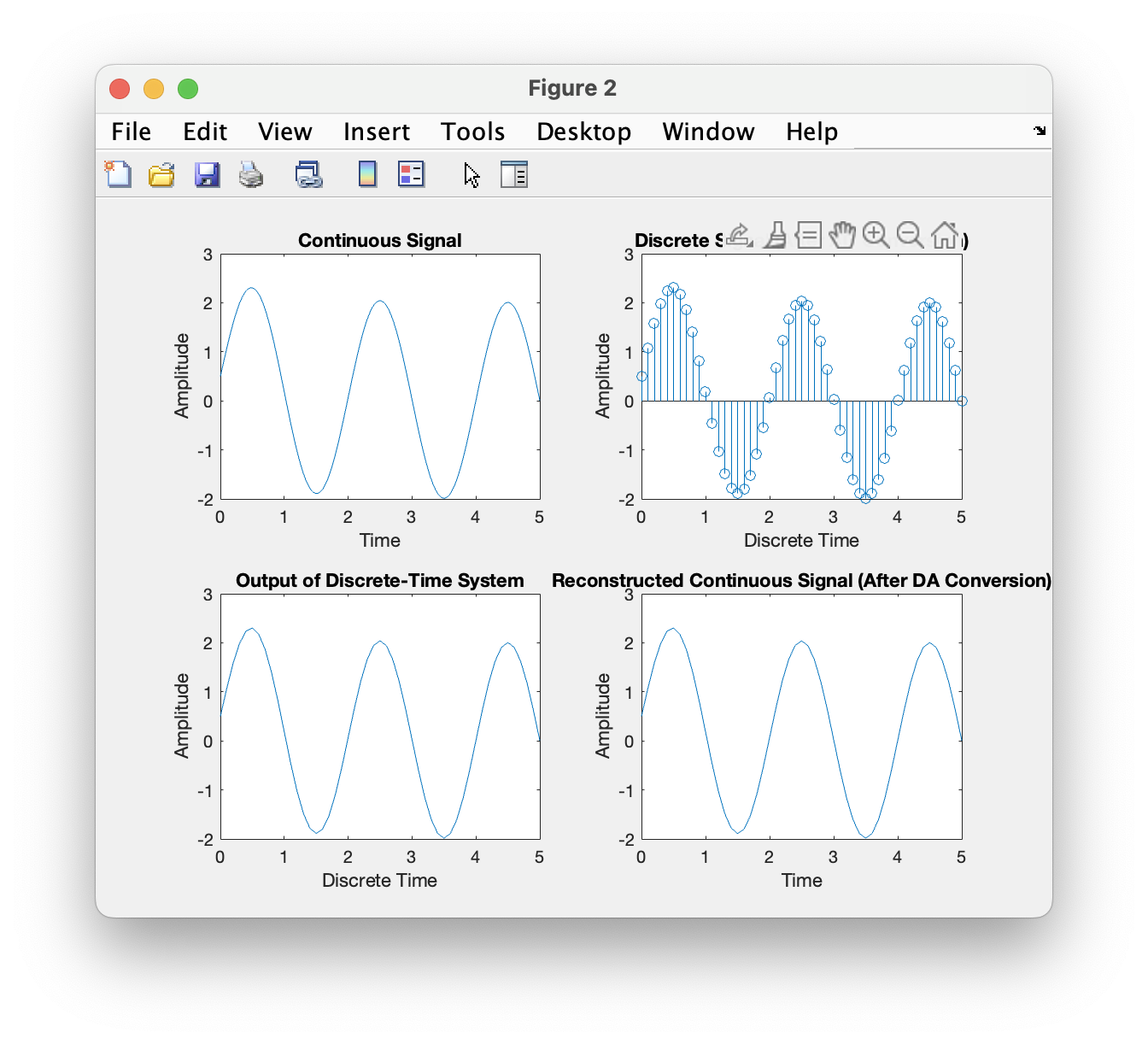
采样率为1时，输出信号严重失真，当采样率为2时其基本信息被保留下来，采样率为10时，信号还原度相对较好。

讨论二

当$h(t)$不为$\delta(t)$时，由于$y(t) = x(t) * h(t)$，卷积为线性运算，不会改变信号的频率，所以仍有：

  
t = 0:0.001:5; % 时间范围
f = 1/2; % 信号频率
x = sin(2*pi*f*t); % 连续信号
y = 2*x + 0.5*exp(-t);

fs = 2; % 采样率
Ts = 1/fs; % 采样周期
n = 0:Ts:5; % 离散时间范围
xd = sin(2*pi*f*n); % 离散信号
yd = 2*xd + 0.5*exp(-n);

t_interp = 0:0.01:5; % 插值时间范围
y1 = interp1(n, yd, t_interp, 'linear'); % 线性插值

% 绘制连续信号
figure;
subplot(2,2,1);
plot(t, y);
title('Continuous Signal');
xlabel('Time');
ylabel('Amplitude');

% 进行AD转换（模拟到数字）
subplot(2,2,2);
stem(n, yd);
title('Discrete Signal (After AD Conversion)');
xlabel('Discrete Time');
ylabel('Amplitude');

% 设计离散时间系统
subplot(2,2,3);
plot(n, yd);
title('Output of Discrete-Time System');
xlabel('Discrete Time');
ylabel('Amplitude');

% 进行DA转换（数字到模拟）
subplot(2,2,4);
plot(t_interp, y1);
title('Reconstructed Continuous Signal (After DA Conversion)');
xlabel('Time');
ylabel('Amplitude');